10x12 Board
Home * Board Representation * Mailbox * 10x12 Board
The 10x12 Board embeds the 8x8 board array, surrounded by sentinel files and ranks to recognize off the board indices while generating moves using offsets per piece and direction to determine move target squares. Two ranks at the bottom and top are necessary to ensure even knight jumps from the corners result in valid array indices greater or equal zero and less than 120.
Contents
Programs
COKO III
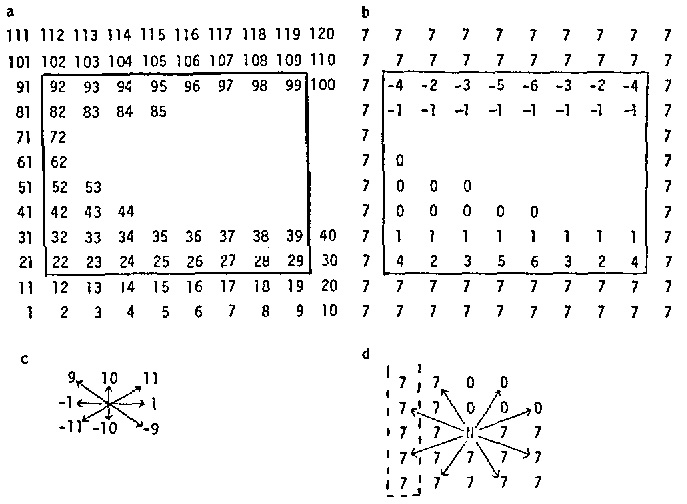
Figure 2 from COKO III: The Cooper-Koz Chess Program (1973) explains COKO's Chess environment [1]:
Chess environment representation: minimal game board. (a) The chessboard represented by a linear array.
(b) Representation of pieces, empty squares and border squares. (c) Move directions for King and Queen.
(d) The Knight dictates that two rows of border squares surround the 8 X 8 game board.
Columns 10 and 1 are considered adjacent.
Sargon
In 1978, Sargon by Dan and Kathe Spracklen used a classical 120 Byte array as board [2] [3]:
; ******************************************************* ; BOARD -- Board Array. Used to hold the current position ; of the board during play. The board itself ; looks like: ; FFFFFFFFFFFFFFFFFFFF ; FFFFFFFFFFFFFFFFFFFF ; FF0402030506030204FF ; FF0101010101010101FF ; FF0000000000000000FF ; FF0000000000000000FF ; FF0000000000000060FF ; FF0000000000000000FF ; FF8181818181818181FF ; FF8482838586838284FF ; FFFFFFFFFFFFFFFFFFFF ; FFFFFFFFFFFFFFFFFFFF ; The values of FF form the border of the ; board, and are used to indicate when a piece ; moves off the board. The individual bits of ; the other bytes in the board array are as ; follows: ; Bit 7 -- Color of the piece ; 1 -- Black ; 0 -- White ; Bit 6 -- Not used ; Bit 5 -- Not used ; Bit 4 --Castle flag for Kings only ; Bit 3 -- Piece has moved flag ; Bits 2-0 Piece type ; 1 -- Pawn ; 2 -- Knight ; 3 -- Bishop ; 4 -- Rook ; 5 -- Queen ; 6 -- King ; 7 -- Not used ; 0 -- Empty Square ; ******************************************************* BOARD = .-TBASE BOARDA: .BLKB 120
TSCP
A textbook example of mailbox board representation is TSCP. The board are two 64 element arrays, containing empty square plus pure piece code, and empty square plus piece color code [4]:.
int color[64]; /* LIGHT, DARK, or EMPTY */ int piece[64]; /* PAWN, KNIGHT, BISHOP, ROOK, QUEEN, KING, or EMPTY */
Square Mapping
The 10x12 versus 8x8 and vice versa square mapping is applied by mailbox and mailbox64 lookup tables. A comment by Tom Kerrigan describes the implementation as follows [5]. However, as pointed out by Harm Geert Muller, not only the embedded 10x12 board, but various implementations are all mailbox, independently from elements in the array for padding that can act as a sentinel value [6] :
/* Now we have the mailbox array, so called because it looks like a
mailbox, at least according to Bob Hyatt. This is useful when we
need to figure out what pieces can go where. Let's say we have a
rook on square a4 (32) and we want to know if it can move one
square to the left. We subtract 1, and we get 31 (h5). The rook
obviously can't move to h5, but we don't know that without doing
a lot of annoying work. Sooooo, what we do is figure out a4's
mailbox number, which is 61. Then we subtract 1 from 61 (60) and
see what mailbox[60] is. In this case, it's -1, so it's out of
bounds and we can forget it. You can see how mailbox[] is used
in attack() in board.c. */
int mailbox[120] = {
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, 0, 1, 2, 3, 4, 5, 6, 7, -1,
-1, 8, 9, 10, 11, 12, 13, 14, 15, -1,
-1, 16, 17, 18, 19, 20, 21, 22, 23, -1,
-1, 24, 25, 26, 27, 28, 29, 30, 31, -1,
-1, 32, 33, 34, 35, 36, 37, 38, 39, -1,
-1, 40, 41, 42, 43, 44, 45, 46, 47, -1,
-1, 48, 49, 50, 51, 52, 53, 54, 55, -1,
-1, 56, 57, 58, 59, 60, 61, 62, 63, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1,
-1, -1, -1, -1, -1, -1, -1, -1, -1, -1
};
int mailbox64[64] = {
21, 22, 23, 24, 25, 26, 27, 28,
31, 32, 33, 34, 35, 36, 37, 38,
41, 42, 43, 44, 45, 46, 47, 48,
51, 52, 53, 54, 55, 56, 57, 58,
61, 62, 63, 64, 65, 66, 67, 68,
71, 72, 73, 74, 75, 76, 77, 78,
81, 82, 83, 84, 85, 86, 87, 88,
91, 92, 93, 94, 95, 96, 97, 98
};
Offset Move Generation
In the offset move generation code, testing if a square is on the board looks as follows [7] [8]:
int side; /* the side to move */
int xside; /* the side not to move */
BOOL slide[6] = {FALSE, FALSE, TRUE, TRUE, TRUE, FALSE};
int offsets[6] = {0, 8, 4, 4, 8, 8}; /* knight or ray directions */
int offset[6][8] = {
{ 0, 0, 0, 0, 0, 0, 0, 0 },
{ -21, -19,-12, -8, 8, 12, 19, 21 }, /* KNIGHT */
{ -11, -9, 9, 11, 0, 0, 0, 0 }, /* BISHOP */
{ -10, -1, 1, 10, 0, 0, 0, 0 }, /* ROOK */
{ -11, -10, -9, -1, 1, 9, 10, 11 }, /* QUEEN */
{ -11, -10, -9, -1, 1, 9, 10, 11 } /* KING */
};
for (i = 0; i < 64; ++i) { /* loop over all squares (no piece list) */
if (color[i] == side) { /* looking for own pieces and pawns to move */
p = piece[i]; /* found one */
if (p != PAWN) { /* piece or pawn */
for (j = 0; j < offsets[p]; ++j) { /* for all knight or ray directions */
for (n = i;;) { /* starting with from square */
n = mailbox[mailbox64[n] + offset[p][j]]; /* next square along the ray j */
if (n == -1) break; /* outside board */
if (color[n] != EMPTY) {
if (color[n] == xside)
genMove(i, n, 1); /* capture from i to n */
break;
}
genMove(i, n, 0); /* quiet move from i to n */
if (!slide[p]) break; /* next direction */
}
}
} else { /* pawn moves */ }
}
}
See also
Publications
- Dan Spracklen, Kathe Spracklen (1978). First Steps in Computer Chess Programming. BYTE, Vol. 3, No. 10, pdf from The Computer History Museum
- David Levy (1979). Computer and Chess - How the monster thinks. Elektor, January 1979 [9]
- Robert Hyatt (1981). Checkmate: The Cray-1 Plays Chess. Part 1. Cray Channels, Vol. 3, No. 1. pdf from The Computer History Museum
Forum Posts
- Board representation : 0x88 or 10x12 ? by Philippe, Winboard Forum, March 02, 2006 » 0x88
- move generation with one dimensional "12 x 10" array by Andrew Short, CCC, August 22, 2008
- mailbox & CPW by Harm Geert Muller, CCC, May 31, 2013
External Links
- Board representation (chess) - Array based from Wikipedia
- Chess board representations by Robert Hyatt
- If - I'm Reaching Out on All Sides, 1970, YouTube Video
References
- ↑ Edward W. Kozdrowicki, Dennis W. Cooper (1973). COKO III: The Cooper-Koz Chess Program. Communications of the ACM, Vol. 16, 7, Fig. 2
- ↑ Dan Spracklen, Kathe Spracklen (1978). First Steps in Computer Chess Programming. BYTE, Vol. 3, No. 10, pdf from The Computer History Museum
- ↑ Sargon Z80 assembly listing by Dan and Kathe Spracklen, hosted by Andre Adrian
- ↑ TSCP - data.c
- ↑ TSCP - data.c
- ↑ mailbox & CPW by Harm Geert Muller, CCC, May 31, 2013
- ↑ TSCP - data.c
- ↑ TSCP - board.c, slightly modified
- ↑ Publication Archive from Chess Computer UK by Mike Watters